O estudo das relações trigonométricas foi fundamental para a disseminação da Matemática. As inovações que surgiram através das relações trigonométricas e suas aplicações são inúmeras e em muitas áreas do conhecimento.

As relações trigonométricas são estudadas com base em um triângulo retângulo(aquele que possui um ângulo de 90°). Vamos lembrar dos nomes dos lados de um triângulo retângulo:

Definindo o Seno de um ângulo

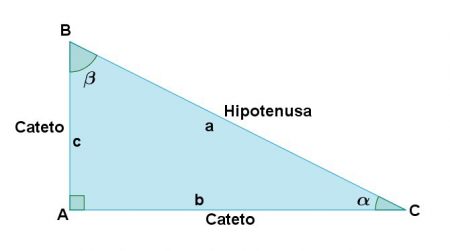
O seno de um ângulo é a razão entre o Cateto oposto a esse ângulo e a hipotenusa. Assim, a relação seno depende do ângulo considerado, veja:

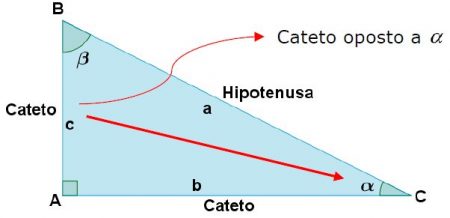
Em relação ao ângulo α:

sen(α)=cateto oposto a αhipotenusa

sen(α)=ABBC

sen(α)=ca

Seno dos ângulos notáveis

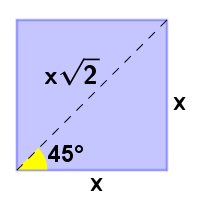
Existem alguns ângulos, que chamamos de notáveis, onde o valor do seno é facilmente calculável, são eles 30°, 45° e 60°. Vamos ver as deduções:

Considere um triângulo equilátero de lado x.

sen(30o)=x2x=x2⋅1x=12

sen(60o)=hx

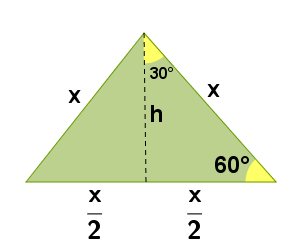
Como o triângulo é equilátero, a medida da altura será: h=x3√2. Assim:

sen(600)=x3√2x=x3√2⋅1x=3√2

Para o sen(45o) teremos:

sen(45o)=xx2√=12√

sen(45o)=12√⋅2√2√=2√2

Podemos organizar a seguinte tabela:

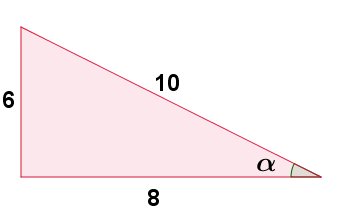
Exemplo prático:

Em um triângulo retângulo a hipotenusa mede 10 e seus catetos medem 6 e 8. O seno de mede?

sen(α)=cateto oposto a αhipotenusa

sen(α)=610

sen(α)=0,6

Função seno

Definimos a função seno como:

f(x)=sen(x)

Lembrando alguns conceitos do Círculo Trigonométrico, fica claro que a função seno tem imagem [-1,1], ou seja -1 ≤ sen(x) ≤ 1, para todo x real.

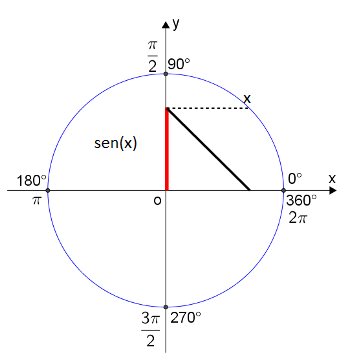
O seno de um ângulo sempre estará sob o eixo das ordenadas (y). Nesse sentido, o seno de um ângulo será sempre positivo no 1º e 2º quadrantes e negativo no 3º e 4º quadrantes

Gráfico da função seno

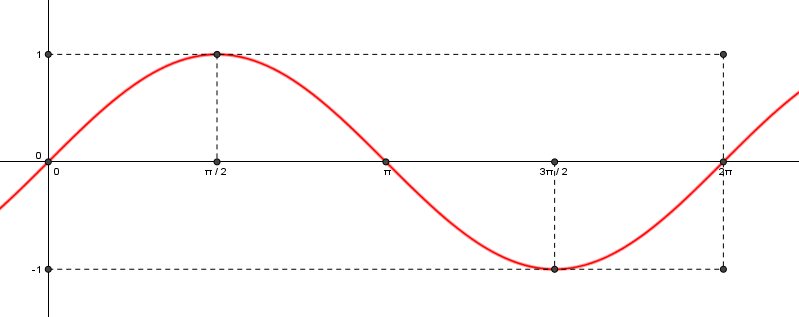
Vamos ilustrar o gráfico da função seno. Para isso, vamos construir uma tabela e, a partir dela, o gráfico:

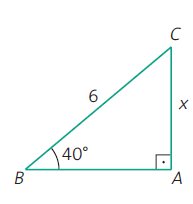
Exemplos

Calcule a medida de x no seguinte triângulo, sabendo que sen(40o)=0,64.

sen(40o)=x6

0,64=x6

x=6⋅0,64

x=3,84

Referências bibliográficas:

DANTE, Luiz Roberto. Matemática: contexto & aplicações. 2. ed. São Paulo: Ática, 2013.

IEZZI, Gelson. Fundamentos de Matemática Elementar. Trigonometria. Vol. 3. São Paulo: Atual, 1995.