Tales de Mileto  foi um grande e reconhecido matemático no período do século VI a.C., seus estudos e descobertas no campo da matemática o fizeram ser taxado como pai da geometria descritiva. Além da matemática, Tales também é lembrado como filósofo e astrônomo

Foto: Reprodução

Sua sabedoria percorreu por vários territórios chegando até o Egito. Os egípcios então, o convidaram a medir a altura de suas pirâmides, o que para a época seria um grande feito, pois não existiam equipamentos que pudessem fazer isso com facilidade. Tales conseguiu medir a altura da pirâmide utilizando hoje o que conhecemos hoje como Teorema de Tales, para conseguir desenvolver este teorema ele utilizou a sombra causada pelo sol e devido a isso sua fama de grande matemático, pensador, ficou ainda maior.

A teoria

O teorema de Tales se dá pela intersecção entre retas paralelas e transversais, onde estas formam seguimentos proporcionais. Tales defendia que a luz proporcionada pelo sol chegava à Terra de forma diagonal, ou seja, inclinada. Foi seguindo essa ideia que ele conseguiu intitular uma situação de proporcionalidade que relaciona as retas paralelas e as transversais. Veja a seguir a imagem para se ter uma melhor compreensão.

Neste exemplo acima, o feixe de retas é formado por três linhas paralelas ( r, s, t) e por duas retas transversais (u, v). Mas outros feixes podem ser formados com mais retas paralelas em um mesmo plano.

O teorema

O teorema de Tales segue a ideia de que, se existem duas retas transversais e estas são cortadas por linhas paralelas, a razão entre quaisquer dos segmentos encontrados em uma das transversais será igual a razão encontrada nos dois segmentos correspondentes da outra transversal.

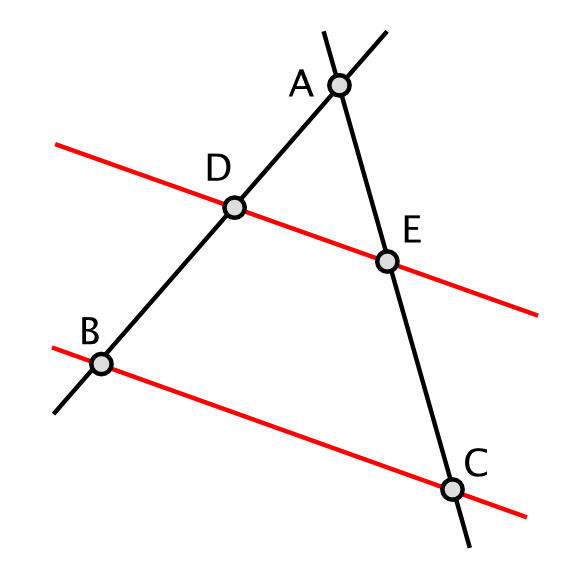
No exemplo dos feixes de retas mostrado acima, de acordo com o Teorema de Tales, podemos encontrar as seguintes razões:

Aplicação do Teorema de Tales

Vamos observar agora alguns exemplos de como se aplica o Teorema de Tales.

Teorema de Tales .

Construção com régua e compasso

Para a divisão do segmento AB em partes iguais ou proporcionais, faça o seguinte:

• Desenhe, a partir de A, dois segmento de reta, que formem um ângulo agudo, reto ou obtuso.
• A partir de Amarque com o compasso duas medidas quaisquer, AE e EC, em um dos segmentos.
• Agora a partir de Ctrace uma reta qualquer que intercepte o outro segmento num ponto B.
• A partir de Etrace uma reta paralela ao segmento BC.
• O ponto Dencontrado divide os segmentos, que concorrem no ponto A, em partes proporcionais.
• Se AEe EC tiverem a mesma medida, então a divisão desenhada também terá partes iguais.

Todas as leituras do desenho geométrico

AD está para AB, assim como AE está para AC.

DB está para AB, assim como EC está para AC.

1. AB está para AD, assim como AC está para AE.
2. AB está para DB, assim como AC está para EC.
3. AD está para DB, assim como AE está para EC.
4. DB está para AD, assim como EC está para AE.

Referências

1. Putnoki, José Carlos - Elementos de Geometria e desenho geométrico. Vol. 1. Ed. Scipione, São Paulo, 1989, p. 112 e 114
2. Mandarino, Denis- Desenho Geométrico, construções com régua e compasso. Ed. Plêiade, São Paulo, 2007, p. 31.